Overview

The MUPS/16 ALU supports 13 basic operations:

• 4 arithmetic operations: ADD, ADDC (add with carry), SUB, SUBB (sub with borrow)
• 4 logical operations: AND, OR, XOR and NOR
• 3 shift operations: SLL (shift left logical), SRL (shift right logical), SRA (shift right arithmetic)
• an EQ operation that uses the carry_out flag to indicate whether the two A and B inputs are equal

All operations operate on two inputs, taken from the A and B busses, and (apart from the EQ operation) produce a single output to the data bus. It's possible to suppress output to the data bus by setting the ~alu_out line high. This is mainly useful for comparisons, where we're interested in the flag outputs (carry_out and less_than), not the result of the computation.

Instruction Details

Instruction	data	carry_out	less_than	Notes
ADD	A + B	1 iff carry out of top bit	undefined
ADDC	A + B + carry_in	1 iff carry out of top bit	undefined
SUB	A - B	0 iff borrow occurred	1 iff A < B
SUBB	A - B - 1 + carry_in	0 iff borrow occurred	undefined
AND	A & B	0	undefined
OR	A | B	0	undefined
XOR	A ^ B	0	undefined
NOR	~(A | B)	0	undefined	Can be used with B input set to Zero register to get ~A
SLL	A << B	0	undefined	No shift-in or shift-out supported
SRL	A >> B	0	undefined	No shift-in or shift-out supported
SRA	A >> B, with sign-extension	0	undefined	No shift-in or shift-out supported
EQ	A - B	1 if A == B, 0 otherwise	undefined

Arithmetic and logic unit

High-level design

The arithmetic and logic units are combined into a single one, using one pair of 4-way multiplexers per bit to perform the logical operations, feeding into 4 sequential 74HCT283 4-bit adders to handle addition and subtraction.

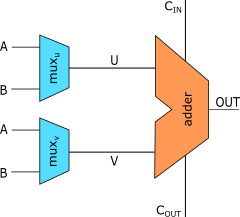
Being able to manipulate inputs before they go into the adder is useful for a variety of operations, as we'll see later.

Logical operations using multiplexers

The logical operations are implemented using 16 4-way multiplexers, using an idea I first saw in the 6502 CPU, and written up in detail here. In short, though, the fundamental observation is that we can turn a 4-1 multiplexer into a programmable logical unit for a single bit. The truth-table for a 4-1 multiplexer with inputs u, v, w, x looks like:

Select input	Output
00	u
01	v
10	w
11	x

Compare this to the canonical truth table for, say AND of two bits A and B:

B input	A input	Output
0	0	0
0	1	0
1	0	0
1	1	1

If we produce the select input for the multiplexer by using a single bit from the A bus and a single bit from the B bus, then we can produce any truth table by varying the values of u-x. For example, to perform an AND of the input bits, we would set u=0, v=0, w=0, x=1. To get XOR, we could set u=0, v=1, w=1, x=0. This means that we can perform any of 16 logical operations with one multiplexers per bit. The complete set of possible operations is:

u	v	w	x	Output
0	0	0	0	0 (constant zero output, regardless of inputs)
0	0	0	1	A & B
0	0	1	0	~A & B
0	0	1	1	B
0	1	0	0	A & ~B
0	1	0	1	A
0	1	1	0	A ^ B
0	1	1	1	A | B
1	0	0	0	~(A | B)
1	0	0	1	~(A ^ B)
1	0	1	0	~A
1	0	1	1	~A | B
1	1	0	0	~B
1	1	0	1	A | ~B
1	1	1	0	~(A & B)
1	1	1	1	1 (constant one output, regardless of inputs)

With this, we can see how to perform the arithmetic and logical operations that the ALU supports.

ADD and ADDC

These are the simplest operations. For ADD we set the control lines for MUXu to 0101, so it passes through A unchanged, set MUXv to 0011, so it passes through B, and set CIN to 0, and we get A+B on the output. ADDC is the same, except we pass the CARRY_FLAG control line to CIN.

SUB and SUBB

Since all we have is an adder, we implement A - B as A + -B. -B in two's-complement arithmetic is just ~B + 1 (where ~B is the bitwise complement of B). We can compute ~B trivially, since it's one of the supported operations in the multiplexers, and we can feed the +1 in by setting CIN to 1. So, to compute SUB, we set MUXu to 0101 (pass through A), set MUXv to 1100 (~B) and set CIN to 1. For SUBB, the only change is that we pass CARRY_FLAG to CIN.

AND, OR, XOR, NOR

To compute these we only need a single set of multiplexers. Since we've set things up so that all output will go through the adder anyway, we simply force the V input to the adder to be 0, by setting MUXv to 0000, so that the U input passes through unchanged. The MUXu lines are just set to the appropriate row from the table above.

EQ

This one is more interesting, and all credit goes to /u/marcelk72 for the idea. The obvious way of determining if A == B is to compute A - B, and test whether the result is 0. This requires dedicated circuitry for the zero detection, which would require 5 additional ICs. Instead, we can use the existing circuitry, and compute A ^ ~B + 1, which will result in a carry out iff A == B. To see why, look at the truth table for A ^ ~B:

A	B	~B	A ^ ~B
0	0	1	1
0	1	0	0
1	0	1	0
1	1	0	1

The result is 1 iff A == B. So, if the inputs are identical, we will end up with a result of 1111111111111111. If we then add 1 to this, the carry will ripple up through all the bits and we'll get a carry out of the result. If any bit is different, there will be at least one 0 bit in the result, which will stop the carry from propagating, and we'll get a carry out of 0. So, for equality detection, the control unit can set OP=EQ and test the carry out for 1.

Summary of logic/adder inputs

Putting all this together, these are the values that we need to set on the MUXu, MUXv and CIN lines for each arithmetic or logical instruction:

Operation	MUXu	MUXv	CIN
ADD	0101	0011	0
ADDC	0101	0011	carry_in
SUB	1010	1100	0
SUBB	1010	1100	carry_in
AND	0001	0000	0
OR	0111	0000	0
XOR	0110	0000	0
NOR	1000	0000	0
EQ	1001	0000	1

Schematics

The overall layout of the arithmetic and logic unit looks like:

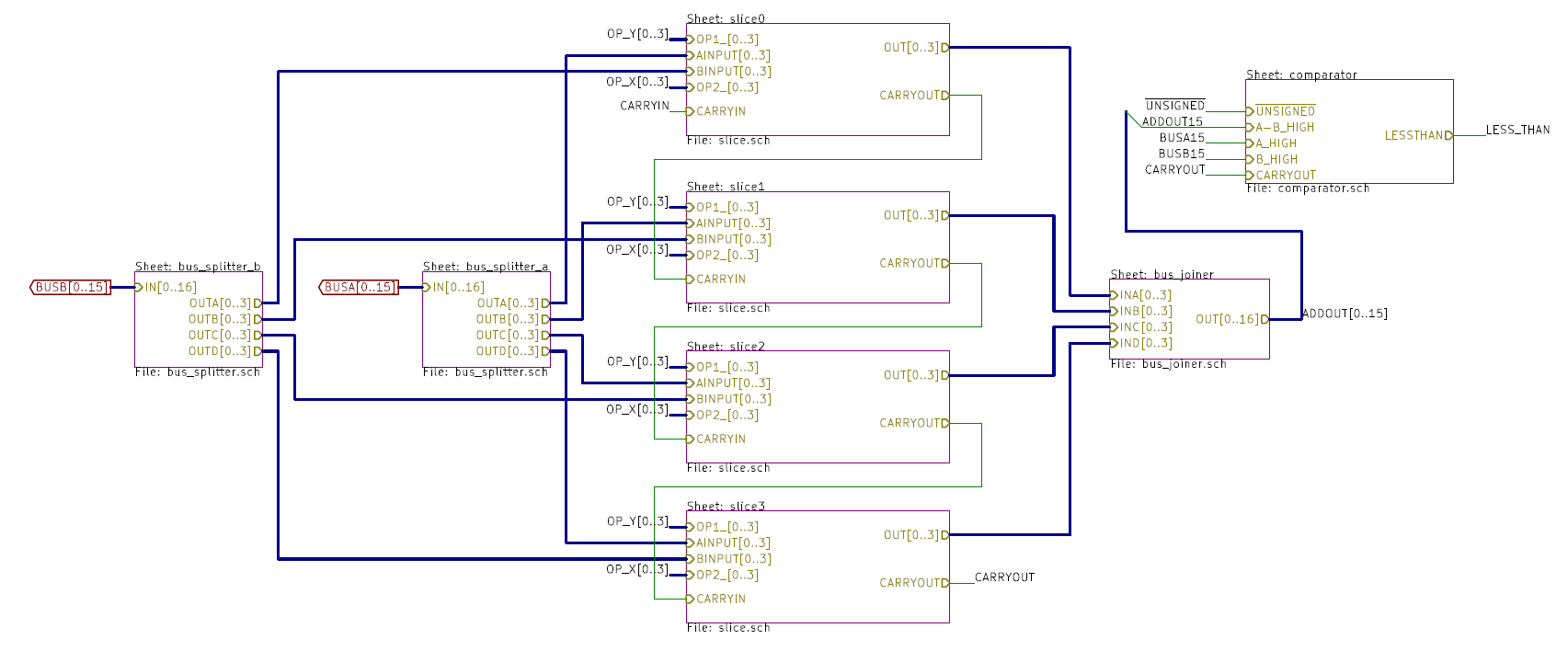
Each slice looks like:

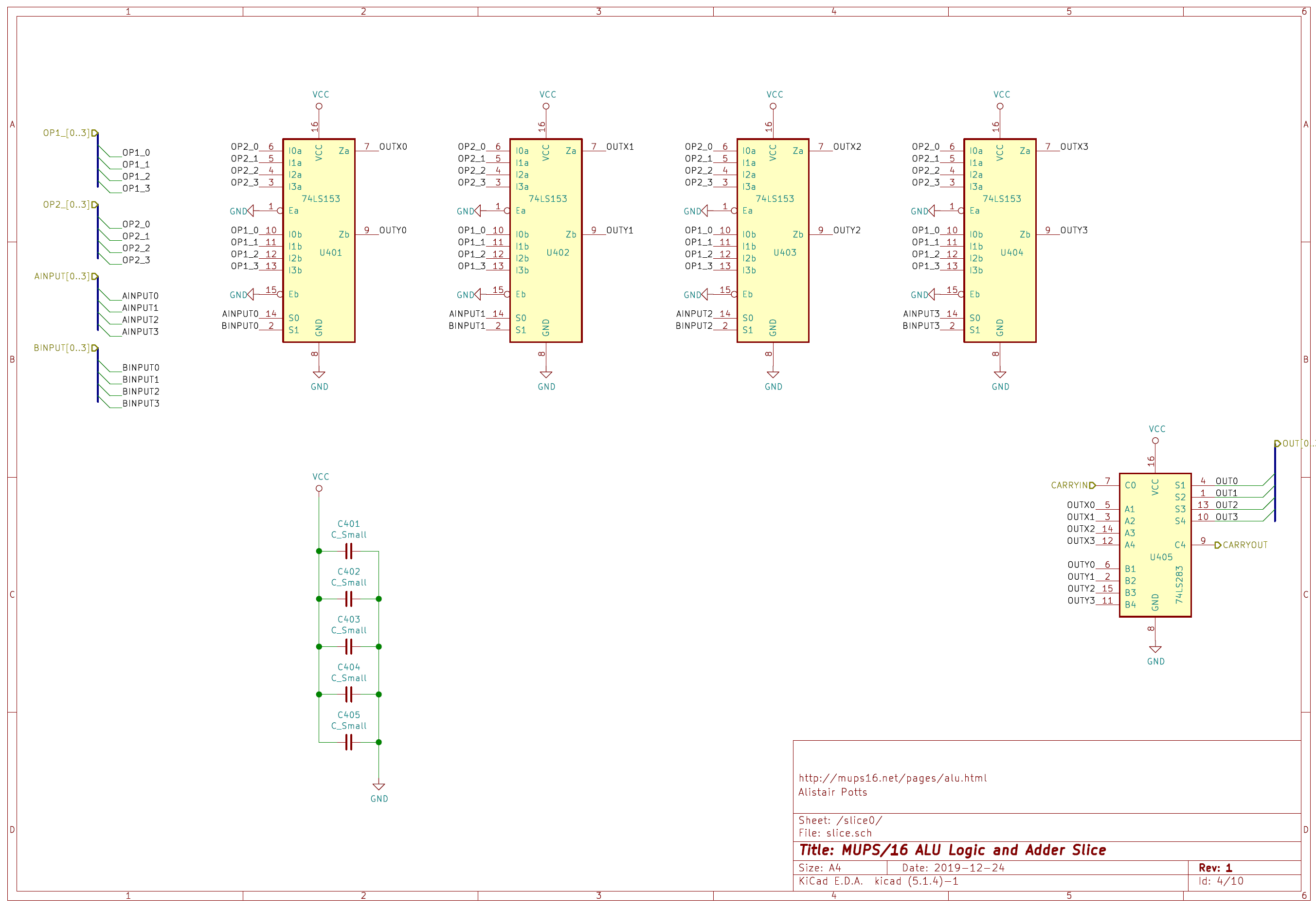
Note that there is a PDF of this image, together with all the other schematics in a single document.

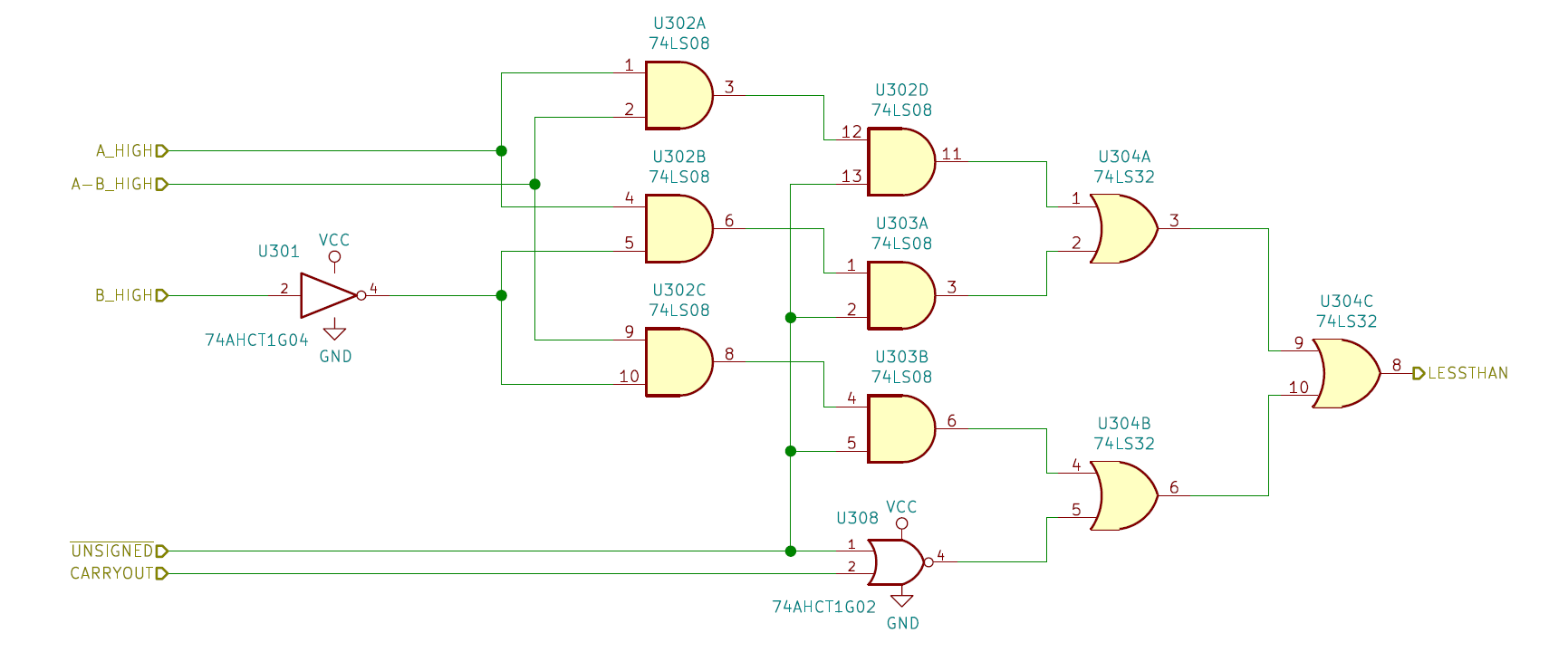
Less-than comparison

A minor operation supported by the ALU is detecting whether A < B. This isn't implemented as a separate operation, but rather appears as an extra output line that is only significant when OP is set to SUB.

For less-than comparison, we have to consider signed and unsigned number separately. Unsigned comparison is very simple. If A < B, then computing A - B will result in a borrow, and so COUT will be 0 (with subtraction, COUT of 1 means no borrowing happened, 0 means we borrowed). Signed comparison is more complicated, as we have to consider the sign of each of the inputs, as well as the sign of the result of the subtraction. Getting the sign of each value is simple enough, as we can just look at the value of the top bit. The possible combinations of signs are shown below:

A	B	(A-B)	A < B?
+	+	+	No
+	+	-	Yes
+	-	irrelevant	No
-	+	irrelevant	Yes
-	-	+	No
-	-	-	Yes

The following circuitry implements the comparison:

Shift unit

High-level design

The shifter is built from has 4 layers of multiplexers, responsible for shifting by 1, 2, 4 and 8 bits respectively. Each layer can switch between on, in which case it outputs its input shifted by an appropriate amount, or off, when it simply passes through its input unchanged. This way we can build up any shift amount from 0..15 by toggling layers. For example, to shift by 9 we would set layers shift1 and shift8 to on, and leave shift2 and shift4 off.

As an illustration, the following shows a very cut-down shifter with only 4 bits, and hence two layers, capable of shifting any amount from 0 to 3 bits.

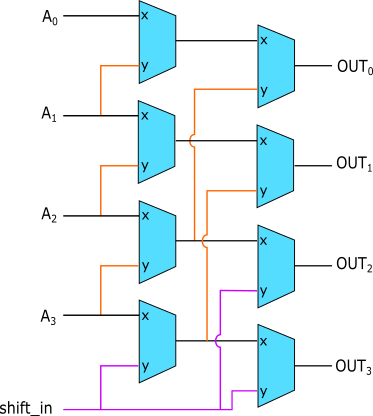
You can see how if we set the the first layer of multiplexers to use their x input, then they will just pass through their output unchanged. If we set them to use their y input, however, then the output of that layer will be SHIFT_IN A3 A2 A1, which has shifted the input right by one bit.

When shifting, we need to decide what to shift into the top bits here. We could decide to shift in the values that are being shifted out of the bottom bits, which would give us bit rotation, but here I've gone for simply shifting in a constant bit, repeated as many times as necessary. Normally, this SHIFT_IN bit will be 0, as this matches the semantics you expect from simple bit-shifting. The only time it will be 1 is if we're doing an SRA operation (arithmetic right shift), in which case SHIFT_IN will be whatever the value of the high bit in the input is.

We could implement left- and right-shifting separately, using two sets of four layers each, and a final layer of multiplexers to choose between the sets. Using the common 74HCT157 quad two-way multiplexers, that would require 4 chips per layer, for a total of 36 chips. We can be slightly more efficient by implementing a right shift by reversing all the input bits, doing a left shift, then reversing the output again. We can implement this with an initial selectable reversing layer, the four right-shift layers, and a selectable final reversing layer, for a total of 24 chips.

There remains the question of how we control each of the shifter layers. Fortunately, that's simple. We wire up all the multiplexers so that 0 on their control line means pass through unchanged. Then, if we assume that we want to shift the value on the A input bus by the value on the B bus, then we can set the control line for the shift-by-1 layer to bit B0, the control line for the shift-by-2 layer to B1, etc. The reversing layers have their control lines set to 1 iff we're doing a right shift.

Schematic

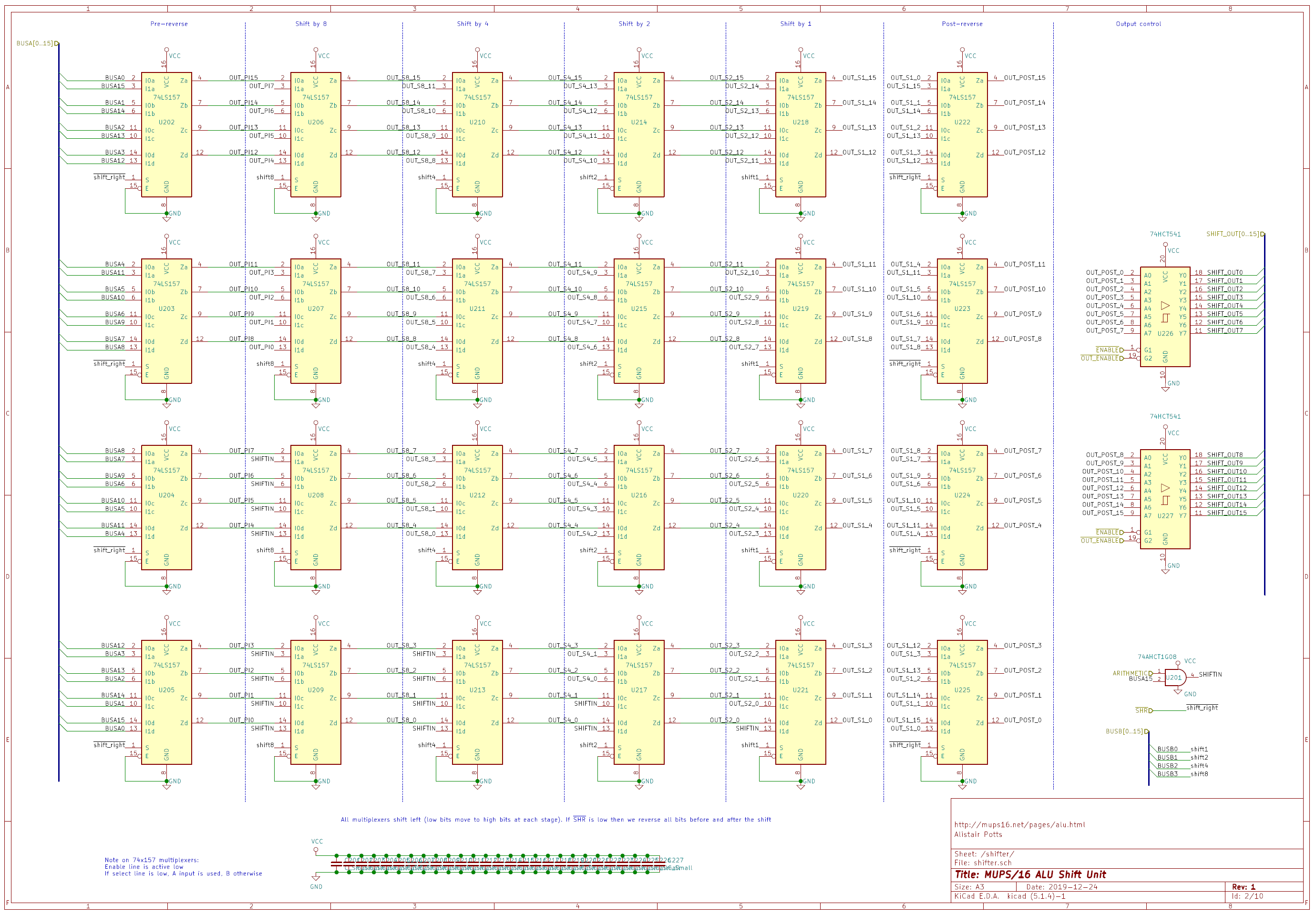
This just reflects the description of the shifter above. You can see the 6 layers of multiplexers, along with a final pair of 74HCT541 bus drivers that allow us to control whether the shift unit should drive the output bus.

Control signal decoding logic

The ALU has 6 control lines:

• OP: 4-bit encoding of the operation to perform
• ~OUT: active-low signal. If low, result of the operation will be asserted to the data bus
• CARRY_FLAG: carry-in bit, used only in ADDC and SUBB operations

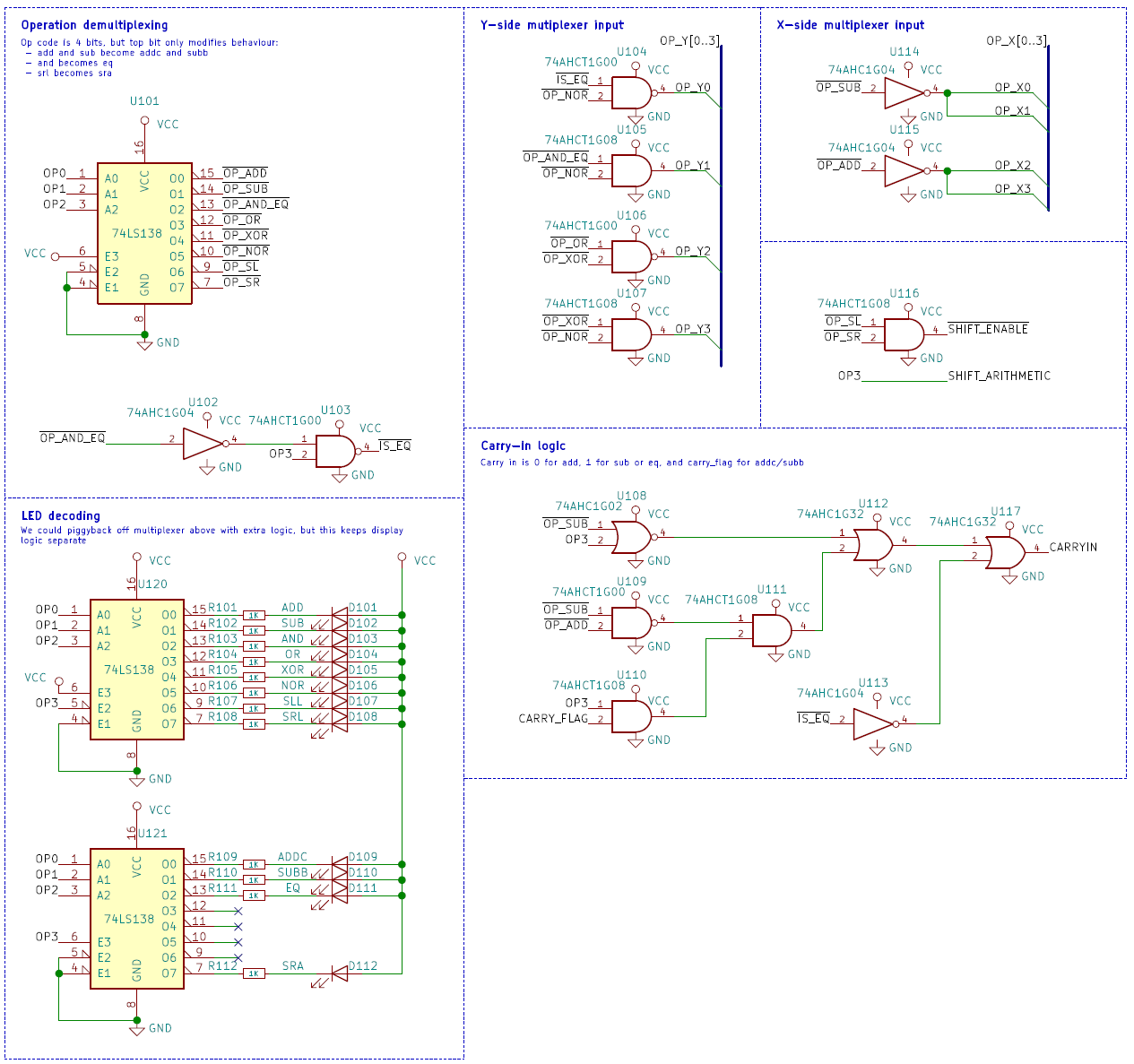
The demultiplexing of the OP lines is split into two parts: one dedicated to producing the LED outputs, for simplicity, and a separate one for the actual decoding. Note that the real decoding only uses the lower 8 bits: the upper bit switches between variants of the same instruction, so ADD becomes ADDC, SUB becomes SUBB, SRL becomes SRA and AND becomes EQ.

The output of the demux feeds into two groups of logic gates, each group producing four sets of internal control signals that drive the multiplexers in the arithmetic/logic unit. Refer to the table above for the values that each of the control signals should have for each operation (note that OP_Y in the schematic corresponds to the control inputs for MUXu in the table above, and OP_X corresponds to MUXv).

The carry_in value for the adders is also computed here, based on the operation and the value of the CARRY_FLAG input.

Thanks

Many thanks to /u/marcelk72 for his help with the equality logic, and to /u/SaltPeppah for pointing out a bug with subb in this writeup.